1 Introduction

The study of neural structure using diffusion-weighted (DW) magnetic resonance imaging (MRI) is relevant for connectivity research and clinical applications. One can infer the local white matter structure by measuring the DW signals along multiple directions. These measurements contribute to the study of brain connectivity patterns and the detection of some brain diseases. For example, the information on the local diffusion directions describing the tissue structure is essential for constructing a diffusion tractography brain model (Nucifora et al., 2007). In diffusion tractography, the method used to infer the intra-voxel structure plays an important role in the quality of the estimation of the anatomy of the human brain (Schilling et al., 2021). In addition, DW imaging is useful for the detection of ischemic stroke, trauma, and brain tumors (Gaddamanugu et al., 2022).

Many models with different characteristics have been developed to recover orientation information from the microstructure of brain tissue. Among them, diffusion tensor imaging (DTI) is one of the most straightforward approaches, based on the Gaussian diffusion model for water movement in biological tissues (Basser, 1995; Soares et al., 2013). DTI approximates the diffusion propagator by a 3–variate normal distribution with a mean of zero, modeled by the diffusion tensor (DT) (Basser, 1995). This model is sound for signals acquired from a single coherently oriented fiber; however, the model is too simplistic for modeling more complex fiber configurations. This is important as ~60 to 90% of diffusion data voxels have fibers that cross, kiss, fan, or bend (Jeurissen et al., 2013), limiting the capabilities of DTI in accurately estimating the microstructure in realistic scenarios. Because of this limitation, several methods have been developed to model the complex fiber configurations of more than one axonal bundle.

Some notable examples of multi-tensor (MT) modeling include diffusion multi-tensor (DMT) modeling for a finite number of orientations (Tuch et al., 2002), Q-ball modeling to reconstruct the diffusion orientation distribution function (Tuch, 2004), constrained spherical deconvolution (CSD) to reconstruct the fiber orientation distribution function (fODF) (Tournier et al., 2007), and non-negative least squares (Ramirez-Manzanares et al., 2007). While DMT generalizes DTI for more than one fiber, the estimation of the fODF via CSD adheres to a non-parametric method. These methods rely on an optimization problem to determine the combination of signals from a dictionary that better reconstructs the measured signal (Tournier et al., 2007). Non-parametric models exhibit more reliability in voxels with crossing fibers (Jeurissen et al., 2011) and depend on fewer parameters than DMT. For these reasons, CSD has been established as one of the most used methods for intra-voxel structure analysis.

However, there are some disadvantages in using traditional methods for intra-voxel structure analysis. For example, CSD is known to provide an overestimation of the number of fibers and it tends to be inaccurate in data with high levels of noise (Jeurissen et al., 2014). To overcome some issues, some improvements to CSD have been proposed. Deep neural networks (DNNs) have recently become a rapidly growing subset of machine learning algorithms that automatically learn the results of interest from data rather than hand-crafted features (Latha et al., 2021). These methods are used to learn models that map the diffusion signal to specific diffusion parameters. Recent studies have shown that DNNs can be competitive with state-of-the-art techniques, improving in areas such as the number of signal acquisitions required for a good estimation, computational complexity, and precision of estimates. Some examples of these methods are LSTM units to extract features as the volume fractions of different compartments (Ye et al., 2019), a U-Net to generate the fractional anisotropy, the mean diffusivity and the fiber tractography (Li et al., 2021), and a multi-layer perceptron (MLP) to address the intricated task of mapping diffusion-weighted signals onto the target fODF (Karimi et al., 2021). In addition, a previous study (Ehrlich and Rivera, 2021) explores the multi-layer perceptron, AxonNet, to estimate the brain nerve bundle orientations and volume fractions for a voxel using data from a small neighborhood around that voxel.

Motivated by the success of DNNs in DW analysis, we propose a novel deep neural network architecture for estimating the orientations and volume fractions of axonal bundles. Our model is based on a self-supervised learning approach: our non-parametric method is implemented by a deep neural network trained with noisy synthetic data. A key feature of our model is the exploitation of spatial correlation between neighboring voxels to improve inference and reduce the number of parameters required. Our model's estimation of orientations and volume fractions achieves competitive results compared to CSDs. It improves the estimation accuracy of images with a high noise level and the angle resolution of the estimated orientations in images with few signals. In addition, for evaluation purposes, we propose using a distance initially introduced in the context of Computational Optimal Transport: the Earth Mover's Distance (EMD) (Monge, 1781). We also discuss the convenience of using EMD over other metrics proposed in the literature. Through some experiments, we show the performance of our model and compare it to CSD using these metrics.

Table 1 lists the acronyms used in this study.

Table 1. Acronyms used in this article.

2 Notation and problem definition

A DW image is a three-dimensional (3D) array of spatially related signals that we denote by S. Each signal, S ∈ S, is a vector of size n, which is assumed to be a sample of a diffusion model. Each entry, Si, is associated with a gradient direction vector gi and a scalar b-value bi. The gradient direction vectors are unitary; that is, |gi| = 1, i = 1, …, n, and the b-values are scalars that depend on the strength, duration, and spacing of the pulsed gradients in the DW acquisitions. The choice of the number of acquisitions, n, the gradient directions and their associated b-value, i=1n, is known as the acquisition protocol of the image. We will use the set notation G=i=1n for its representation.

For a given measure, S ∈ ℝn in S, our interest is to provide information about the tissue's microstructure corresponding to this signal. In particular, we characterize the structure by determining the number of axonal bundles, their orientations, and their contribution to generating the signal S. We denote these values as k, i=1k, and i=1k, respectively. We usually use the term fibers to refer to the axon bundles and their contributions to the signal as volume fractions. For the estimation of these data, we assume that there exists a function, F, so that

for some random noise, ϵ, usually modeled through a Rician distribution (Gudbjartsson and Patz, 1995). Unfortunately, the transition from S to , is an ill-posed problem.

2.1 Brief review of theoretical models

For a voxel with a single fiber, the preeminent approach used to delineate F is the widely embraced diffusion tensor (DT) model, as documented in the study of Basser (1995). The DT is defined as

S(gi,bi)=S0e(−bigi⊤Dgi);

in which the unknown variable D ∈ ℝ3 × 3 represents the covariance matrix of diffusivity. At the same time, S0 denotes the measured signal obtained without diffusion weighting (i.e., when the b-value is zero). The fiber orientation is recovered from this model by computing the larger eigenvector of D; that is, the eigenvector associated with the larger eigenvalue. This vector signifies the orientation of higher diffusivity and is expected to be aligned with the fiber orientation.

As mentioned in the introduction, according to some authors (Ferizi, 2014), most of the diffusion data correspond to signals of more than one fiber crossing. To model these complex signals, numerous methods have been introduced; for example, DMT (Tuch et al., 2002), CSD (Tournier et al., 2007), and NNLS (Ramirez-Manzanares et al., 2007). They can be broadly categorized into two main types: parametric and non-parametric approaches.

A popular example of a parametric model is the diffusion multi-tensor (DMT) model (Tuch et al., 2002). DMT is a linear combination of t simple diffusion tensors in the same model, each with its corresponding parameters, that model a signal of crossing fibers. The DMT model is expressed as follows:

S(gi,bi)=S0∑j=0t(-bigi⊤Djgi).

In the case of non-parametric approaches, two of the most popular methods are non-negative least square (NNLS) (Ramirez-Manzanares et al., 2007) and constrained spherical deconvolution (CSD) (Tournier et al., 2007). Both are based on an optimization problem to determine the combination of signals from a dictionary that better reconstructs the original signal. This dictionary can approximate the orientation and volume fraction of the underlying fibers.

Formally, the NNLS problem can be defined as follows:

x*=argminx∥Ax-y∥2subject to x≥0

where A ∈ ℝm×n is the fixed dictionary of diffusion signals, y is the data vector, and x* ∈ ℝm is our vector solution.

The original CSD method (Tournier et al., 2007) assumes that the diffusion signal within a voxel can be modeled as a sum of spherical functions, each representing the contribution of a different fiber orientation. These spherical functions are convolved with a response function characterizing the point spread function of the image acquisition. The estimation process involves solving a sequential quadratic objective minimization problem:

xt+1=argminx∥Ax-y∥2+λ||L⊤x||2.

In this formulation, x represents the fODF coefficients, y is the observed diffusion signal, A represents a linear combination of spherical basis functions (often using spherical harmonics of order zero), and L is a penalization matrix that penalizes negative contributions of the estimated signal at each direction of the basis functions. The objective function minimizes the difference between the estimated signal (Ax) and the observed signal (y) while applying a regularization term to enforce constraints on the estimated fODF. The regularization parameter λ controls the strength of the regularization.

3 Materials and methods

In this study, we propose a non-parametric method for intra-voxel structure analysis. It consists of a model that infers the number of fibers, their orientations, and their volume fractions. For this purpose, we propose to employ a neural network whose expected output is interpreted as a discretized fODF over a dictionary D of d orientations. The network is trained using synthetic data generated by the DTM model, and the training is self-supervised. This section describes the model's architecture, the synthetic data generation, and the training procedure.

3.1 Model overview

Our model builds upon four fundamental principles, each contributing to its effectiveness. First, it exploits the additional information derived from neighboring signals to enhance the prediction accuracy of a voxel's microstructure. Second, it incorporates a specialized architecture designed to process neighboring signals while maintaining reasonable trainable parameters. Third, we introduce a procedure for generating a synthetic dataset that is simple but realistic enough to ensure the neural network's correct training. Finally, encoding the orientations and volume fractions to create the ground truth targets facilitates our network's seamless training.

As previously mentioned, our model exploits the spatial correlation of neighboring voxels. Two observations support the idea of using this additional information. First, the fiber orientations are expected to change moderately in neighboring voxels, as suggested in various tractography studies (Nucifora et al., 2007). Second, if the noise in each voxel is assumed to be uncorrelated (Salvador et al., 2005), different noise levels are present in each voxel, altering the inference. Therefore, a group of neighboring signals around a central voxel could provide more information about the orientation of the fibers and effectively average out the noise, improving the structure's inference.

It is important to note that ours is not the first method to consider using information from adjacent voxels for this task. For instance, Lin et al. (2019) proposed a model incorporating first-order neighboring voxels for inference. Furthermore, a previous study (Ehrlich and Rivera, 2021) showed that incorporating neighborhood information as input for multi-layer perceptrons improves prediction quality. In light of these findings, we have designed our neural network to accept a 3 × 3 × 3 voxel patch as input, enabling the inference of the structure of the central voxel within the patch. Concerning the neighborhood size, one could be tempted to define a larger neighborhood as this incorporates more information into the model; however, increasing the size compromises the network's efficiency, and this new information might not improve the result. Thus, we decided to use the smallest neighborhood that could contain all the possible orientations the fibers in the central voxel can take, covering a volume of 0.216cm3.

Despite the benefits of considering more voxels to improve the inference, this decision comes with the trade-off of processing a larger volume of signals. In our case, the input data expand from a single voxel to 27 voxels. This expansion also impacts the design of the neural network as a change in the input data size typically necessitates an increment in the number of neurons in subsequent layers (Xu and Chen, 2008). For example, Ehrlich's neighborhood configuration of the AxonNet (Ehrlich and Rivera, 2021) employs a multi-layer perceptron (MLP) with seven layers and nearly 20 million parameters to handle the increased input size. To tackle this challenge, we can use other types of architecture more appropriate for spatially correlated data.

One approach that tackles this drawback is to use a convolutional neural network (CNN). Some studies show experiments using this type of network (Lin et al., 2019; Aliotta et al., 2021). However, the convolutional layers impose a strong assumption about the relationship between neighboring signals and the structure we want to uncover. The convolutions are linear operators on the underlying data, designed to learn low levels of abstraction. As we know nothing about how the relationship of the signals can be uncovered, we believe that replacing the simple convolutions with a more expressive non-linear function can improve the local model's abstraction capability.

3.2 Neural network architecture

In this study, we introduce a novel architecture to solve the problem. Our proposal uses the same parameter-sharing scheme of CNNs but follows the idea proposed by Lin et al. (2013). This relies on the same assumption as CNNs: If one feature is useful for inferring the structure at some spatial position, it should also be useful at a different position. However, instead of convolutional layers, we use perceptrons: a well-studied function approximator (Mcculloch and Pitts, 1943). With this change, we assume nothing about the type of relationship between neighboring voxels that is relevant to infer the intra-voxel structure. Nevertheless, as with CNNs, the same dense network is shared between regions of voxels by dragging it over the input data.

The network consists of three layers as illustrated in Figure 1. We adopt the idea of Lin et al. (2013) in the first two layers of the network. The first layer is dense with ReLU activation functions, fed by a chunk of 2 × 2 × 2 voxels. The output of this layer is a vector of size n1 that we interpret as a feature vector, or descriptor, of the input neighborhood. As the full patch taken by the model is a cube of 3 × 3 × 3 voxels, each with m signals, it is possible to take eight blocks of size 2, each one taking a different corner, to be processed by the first layer, as it is portrayed in the first part of Figure 1. Following this procedure, after the first layer, we get eight vectors that we arrange graphically as a cube of size 2 × 2 × 2, with each voxel of size n1. Note that the eight descriptors obtained from the first layer were built by considering 2-voxel-sized neighborhoods containing the central voxel. Therefore, we expect the descriptors to include structural information of the central voxel based on the direction toward which the neighboring voxels are biased. We think this information should help the model to infer the struture of the central voxel.

Figure 1. Diagram showing our NN's architecture proposal and how it evaluates a datum, represented as a cube of voxels.

For those familiar with convolutional neural networks, the evaluation mechanism of the first layer can be expressed in convolutional terms. This first part of the network can be seen as a 3D-convolutional layer that uses n1 filters of size (2, 2, 2) to process data of size (3, 3, 3), with m channels (the number of signals), at a stride of 1. The output is then evaluated in a ReLU activation function. The second layer of the architecture works as the first one with a few changes. This layer takes the descriptors generated in the first layer. Still, as there is only one chunk of size 2 × 2 × 2, the output is a vector of length n2 that encompasses the information needed for the inference (see the middle part of Figure 1). As in the previous layer, ReLU is used as an activation function. The resulting vector is then passed to a linear layer and evaluated in a Softmax activation function. The inference consists of a vector of size |D|. This output can be interpreted as a probability vector over the dictionary of orientations, D. Ideally, the desired output should be Dirac deltas over the orientations, with intensities representing the volume fractions.

Observe in Figure 1 how, even though we consider a neighborhood as input for the model, the number of layers is manageable: there are only three layers! This is because the first two layers, albeit dense, are shared by the small neighborhoods of the 3D image, reducing the complexity of the model. Moreover, we can extend the same architecture to larger neighborhoods for images with smaller voxels by adjusting the stride and the number of layers. Table 2 exemplifies the various configurations that can be arranged. For instance, if we consider a neighborhood of size 5 × 5 × 5, we can use a first layer with a stride of 1, a second layer with a stride of 2, and a third layer with a stride of 1 outputting 4 × 4 × 4, 2 × 2 × 2, and 1 × 1 × 1 neighborhood representations, respectively.

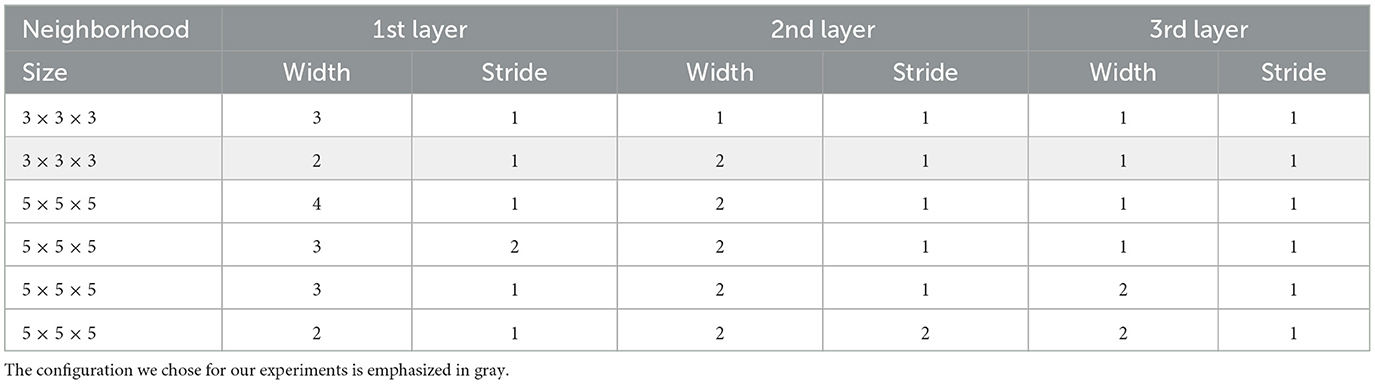
Table 2. Possible configurations of our architecture.

Note that the first two options in Table 2 correspond to known models; the first is an MLP architecture with two hidden layers, and the second configuration is the proposed architecture. By recycling the same perceptron to process all the small neighborhoods, we could reduce the network's complexity compared to AxonNet (Ehrlich and Rivera, 2021). In addition, when processing a complete DW image, the first layer can independently process the small neighborhoods of size two, allowing each to be processed in parallel.

3.3 Synthetic data generation

An important part of our model is generating the training data. Given that medical images lack ground truths, our neural network is trained using only synthetic data, conforming our model to a self-supervised method. According to our results, auto-generated data are sufficient for the correct model generalization. Although there are many complex modes for representing a DW signal, for the synthetic data generation, we used a Gaussian diffusion model for being simple and computationally efficient. Therefore, the synthetic data generation consists of defining the variables for the diffusion multi-tensor model, simulating the signals using the DMT model, and generating the representation of the variables to predict. We generate realistic training and validation datasets according to the acquisition protocol of the real DW–signals to be analyzed. Our procedure is described in the following steps.

3.3.1 Fiber representation

We randomly set the orientations of three synthetic fibers for the central voxel; this is done by taking three points uniformly over the unit sphere. Then, vectors whose angular distance is less than min_deg are considered a single fiber. Thus, the number of fibers can be less than three. For all datasets, we set min_deg to 20 degrees.

To set the volume fractions of the previously generated fiber orientations, we follow these steps:

1. We draw two numbers from a uniform distribution u1,u2~U[0.1,0.9].

2. We denote the volume fractions corresponding to each of the three fibers, f1, f2, f3, and they are defined as follows:

f1 = min(u1, u2)

f2 = |u1−u2|

f3 = 1−f1−f2

3. We set to 0 the volume fractions corresponding to non-existing fibers, due to the min_deg constrain, and renormalize the values so that f1+f2+f3 = 1.

This way, we can generate voxels containing up to three fibers. Because of step three, ~68% of our dataset contained three fibers, 30% contained two fibers, and a few contained only one fiber. We tried other configurations of these proportions and found no evidence of improvement in the results. We just observed that to predict the three-fiber scenario correctly, the network needed more than half of the data corresponding to that case, given that this scenario seems more challenging. Therefore, we decided to keep these percentages.

3.3.2 Neighborhood generation

We build neighborhoods that diverge slightly from the previously generated central voxels to complete the training and validation datasets. For such a purpose, we do the following:

• We add random perturbations to the vectors generated for the central voxel to form eight different perturbated copies, one for each corner of the 3 × 3 × 3 neighborhood. The perturbations are made by adding small values to the Euler angles defining the tensors, sampled from N(0,0.25)

• We set the fibers of the rest of the neighboring voxels using trilinear interpolation.

• The volume fractions are not modified for any of the neighboring voxels.

Under this procedure, a neighborhood of 3 × 3 × 3 voxels. The corresponding ODF of one datum is shown in Figure 2, where we observe the directions of the three fibers in the 27 voxels of the neighborhood.

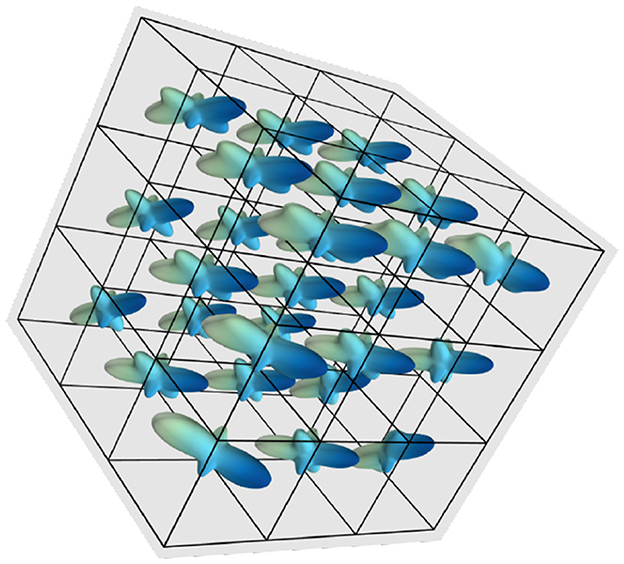
Figure 2. fODF depiction of a datum in the training data, corresponding to a neighborhood of voxels spatially correlated.

3.3.3 Signal simulation

The signals are generated using a DMT model with a tensor eigenvalue calibrated from the corpus callosum of an actual DW image (the one used in the qualitative analysis), using the same acquisition protocol G as the real DW signals to be analyzed. This is the bottleneck of the proposed self-supervised approach because of the time it consumes. Fortunately, this generation only needs to be done once for each protocol.

As the image intensity in magnetic resonance images in the presence of noise is shown to be governed by a Rician distribution (Papoulis, 1984; Gudbjartsson and Patz, 1995), we add random Rician noise to the signals of our training and evaluation sets. The noise added is controlled by the signal-to-noise ratio (SNR). First, we randomly choose an SNR into the interval [15, 35] for every datum. With this variation in the noise, we expect the model to generalize well for different DW images. We admit that the choice of this model biases the signals generated using the DMT model. Although these effects are especially noted in the case of neural networks (NN), they are not particular to them. We can say that they are general: Models such as CSD or NNLS generally use the response of the prototype voxel in the corpus callosum (adjusting a mono-tensor) as an element to build the (discrete) signal dictionary. We have tried to ensure this training database is large enough to mitigate this bias. Still, we accept this limitation because the model is designed to be trained with synthetic data due to the scarcity of ground truths in medical images. Nevertheless, as demonstrated in previous studies, we believe the approach can generalize well to actual data (Ehrlich and Rivera, 2021; Karimi et al., 2021).

3.4 Ground truth labels

We already mentioned that the desired output is a vector of responses to a dictionary of orientations D of size d. To define the ground truth labels, we must define D. The dictionary contains vectors indicating orientations. We set all vectors in the upper hemisphere (positive third dimension) for convenience. To cover most orientations, the vectors are as equally distributed as possible (Jones et al., 1999). An ideal dictionary should have as many orientations as possible to minimize errors, but with 362, we get an excellent level of precision. Now, we define the representation we will use for the output data. The output representation must encode the multiple fibers of the central voxel and their volume fractions. We interpret the output of the model as the volume fractions distributed in the d orientations given in the dictionary D. Therefore, as in many deep learning applications, the ground truths, called here labels, should reflect that. To that aim, the labels of the central voxel are crafted using a two-step procedure.

In the first step, we compute the Nearest Element (NE) of the dictionary for every fiber orientation in the central voxel; that is, we compute the element in D that has the smallest angle to the vector representing the fiber orientation. After computing these labels, we scale them by their volume fractions. Formally, for an orientation v, the Nearest Element label of v is defined as

LNE(v)=fvargmind∈Darccos(|v⊤d|),

where fv is its corresponding volume fraction.

The nearest element labels are our desired output, but choosing this representation introduces a 0–1 loss in training a neural network: Either the model's predicted orientations are right or wrong. However, not all orientations are necessarily wrong since good approximations of the orientations are more desirable than others with a larger angular distance. Therefore, we introduce a more sophisticated representation that encodes a confusion matrix on the orientations. This representation reduces the penalty for small orientation errors. We refer to these labels as Watson Labels as they are constructed by adjusting a Watson distribution discretized by the orientations in the dictionary with center on the Nearest Element labels. More formally, we build these labels under the following formula:

where Wσ ∈ ℝm×m is the confusion matrix containing the weights of Gaussian blurring on the sphere with variance σ. Given two directions in the dictionary, d~i,d~j, such weights are defined as Wi,jσ=w(dθ(d~i,d~j))w(0) for w(a)=1σ2πe-(aσ2)2, the evaluation of the angles between dictionary directions on a Watson density distribution. LWσ are shown graphically in Figure 3. Note that if a voxel contains just one tensor with direction d, this construction will do the labels equal to their evaluation on a Watson distribution with mean d and variance σ. For more than one fiber, the sphere displays a mixture of Watson distributions with the center in the NE labels, pondered by the volume fractions. Formally, given the Watson blurring of three orientations, LWσ1,LWσ2,LWσ3, the final labels are defined by the following mixture of Watson distributions:

LWσ=∑i=13LWσi for i=1,2,3.

For convenience, σ is expressed in degrees but converted to radians for the computations. In our experiments, we noticed that small values are difficult to train and generate a greater angular error, while a large σ produces less quality in the volume fractions estimations. In this study, values of 8° and 10° are used to construct the Watson labels, LW8 and LW10, respectively.

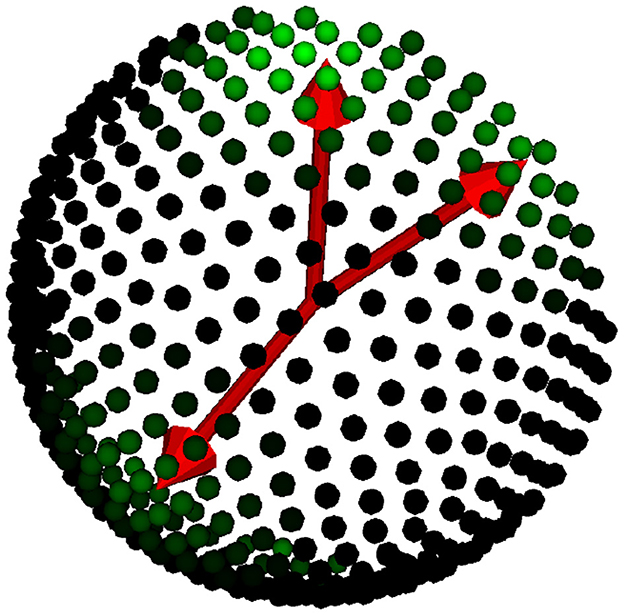
Figure 3. Watson label representation over the dictionary. We display the true orientations in red, while the Watson labels are shown as green intensities over the dictionary of orientations in the hemisphere.

In case of analysis of ultra-high field data, our method accepts that training data and diffusion labels can be generated with non-Gaussian diffusion models, as the revised by Gallichan (2018), with a slightly additional computational cost.

3.5 Training

We train the network with the mean squared error (MSE) loss function between the output tensor and the ground truth labels. This error for two vectors x, y ∈ ℝm is defined as

where x are the normalized signals. MSE is the loss function used per excellence for regression problems when training neural networks. This is due to the equivalence of minimizing the quadratic norm to the maximum likelihood estimator by assuming a Gaussian distribution for the noise. Although many specific loss functions exist for different tasks nowadays, MSE typically exhibits good training accomplishments. This study is not the exception; we use MSE as a loss function to train our models.

The optimizer used for training was Adam, with a learning rate of 0.002. We decreased this learning rate by a factor of 0.2 when reaching a plateau in the training loss. The training was stopped when the loss, computed in an independent validation set, did not decrease for 10 epochs. No regularization was used. The training set consisted of 20,000 examples, and the validation set consisted of 5,000 examples of 27 voxels generated with the procedure introduced in the previous section. The number of signals depends on the acquisition protocol of the evaluation's datasets.

3.6 Experimental methodology

The experiments were focused on determining the quality of the inferences produced by our model. To that end, we tested how well it can infer three crucial elements of the intra-voxel structure: the number of fibers, their orientations, and the volume fractions. For this purpose, we conducted some experiments and used several metrics. We describe the experimental setup in this section.

Our experiments are divided into two parts according to the objectives pursued. The first set of experiments tested how the different hyperparameters affected the model's prediction. These values are the number of neurons in each layer, n1 and n2, and the parameter σ, the variance of the Watson distributions used for the labels. We also validated the model by comparing its performance with classical MLPs. When choosing the size of the layers, we were interested in a model with a low computational complexity without compromising good performance in the precision of the inference. For the validation of the model, our reference is the Multi-Layer Perceptron AxonNet (Ehrlich and Rivera, 2021), as a previous study suggested a good performance. To that aim, we consider the predictions of the two MLPs:

• A MLP consisting of seven linear layers with neurons ranging from 512 to 4,096. This model takes the voxel's neighborhood as input, just as our proposed model. For the rest of this study, we refer to this model as Neighborhood-MLP.

• A MLP that evaluates the signals of the central voxel, ignoring the neighboring voxels. This slightly smaller model has six dense layers and a range of neurons between 512 and 2048. We refer to this model as the Voxel-MLP.

We refer to Ehrlich et al. in 2020 preprint (Ehrlich and Rivera, 2021) for more detailed information about these models.

The second set of experiments was conducted to test the performance of our model in a well-known phantom image and compare our estimations with the estimations produced by CSD. To that end, we evaluated both models using simulated data given as evaluation on the ISBI 2013 HARDI reconstruction challenge (ISBI, 2013). The signals of this phantom image were simulated through a more complex procedure that differs from the one used for the training data. The data consist of images of size 50 × 50 × 50, and it is available in two acquisition protocols: a DTI scheme with 32 signals and b-values of 1200 s/mm2, and a HARDI scheme with 64 directions and b-values of 3000 s/mm2. We concatenate both images for our experiments, producing a multi-shell protocol of 96 signals. As the ground truth fixels are given for each voxel, we can evaluate the quality of the predictions. The quantitative evaluation consists of several metrics over the fODFs estimated by each model and the time each model takes to produce the estimations. One crucial element for the comparison is the metrics used to evaluate the models. We dedicate the following section to introduce those metrics.

Finally, our experiments are completed with a visual inspection of the estimations on data from a real healthy male subject from the Stanford HARDI dataset (Rokem et al., 2015). The set consists of single-shell data with b-values of 0 and 200 s/mm2, with a protocol of 160 gradient directions. In this inspection, we focused on evaluating the predictions on areas with multiple crossing fibers and some common mistakes in the estimations found in the literature.

3.7 Performance metrics

We can assess several aspects in measuring the quality of the inferred microstructure. For instance, Canales-Rodŕıguez et al. (2019) compiled five types of error that can be taken into consideration to evaluate the precision of the estimated peaks: the angular error, the volume fraction error, the number of fibers over-estimated, the number of fibers under-estimated, and the success rate. A fiber peak is an estimated fiber orientation chosen from an orientation distribution function and associated with a volume fraction. To evaluate the precision in fiber orientations for a datum, they propose the angular error defined as

θe=1Mtrue∑k=1Mtrueminm,

where Mtrue is the true number of fiber populations; em is the unitary vector along the m-th detected fiber peak, and vk is the unitary vector along the k-th true fiber orientation.

In addition, Canales-Rodŕıguez et al. (2019) proposed using the mean absolute error as a volume fraction error:

Δf=1Mtrue∑k=1Mtrue|fm-fk|.

To evaluate how well a model estimates the number of fibers, Canales-Rodŕıguez et al. (2019) propose computing the mean number of fibers over-estimated per voxel, n+, and the mean number of fibers under-estimated, denoted by n−. In addition, the cited study defines the Success Rate, SR, as the proportion of voxels in which the algorithm estimates the right number of fiber compartments, calculated with an angular error inferior to a given value (25° in our experiments), and the correct relative order of volume fraction among the predicted fibers. The Success Rate is a metric that indicates the accomplishments in the estimation. In Figure 4, we observe how small variations in the solution produce unsuccessful estimations.

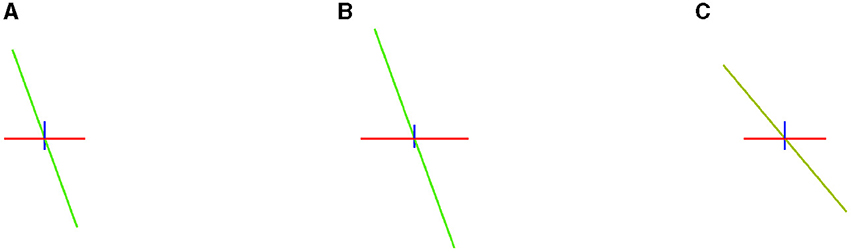
Figure 4. Example of how small differences in estimation can produce an unsuccessful estimation. In the left image (A), three vectors of volume fractions of 0.5 (blue), 0.35 (green), and 0.15 (red). In the center (B), the same vectors but with volume fractions of 0.4, 0.41, and 0.19, a different relative order of predominance. In the right-hand image (C), the same volume fractions but a vector with a distance of 20.1° w.r.t. the first image.

Canales-Rodŕıguez et al. (2019) propose a metric that considers the errors mentioned above to facilitate the comparisons between different methods. The global relative performance (GRP) of a method i is defined as

GRP(i)=θi〈