Objective. Explore the application of Haralick textural analysis to 3D distributions of specific energy (energy imparted per unit mass) scored in cell-scale targets considering varying mean specific energy (absorbed dose), target volume, and incident spectrum. Approach. Monte Carlo simulations are used to generate specific energy distributions in cell-scale water voxels ((1 μm)3–(15 μm)3) irradiated by photon sources (mean energies: 0.02–2 MeV) to varying mean specific energies (10–400 mGy). Five Haralick features (homogeneity, contrast, entropy, correlation, local homogeneity) are calculated using an implementation of Haralick analysis designed to reduce sensitivity to grey level quantization and are interpreted using fundamental radiation physics. Main results. Haralick measures quantify differences in 3D specific energy distributions observed with varying voxel volume, absorbed dose magnitude, and source spectrum. For example, specific energy distributions in small (1–3 μm) voxels with low magnitudes of absorbed dose (10 mGy) have relatively high measures of homogeneity and local homogeneity and relatively low measures of contrast and entropy (all relative to measures for larger voxels), reflecting the many voxels with zero specific energy in an otherwise sporadic distribution. With increasing target size, energy is shared across more target voxels, and trends in Haralick measures, such as decreasing homogeneity and increasing contrast and entropy, reflect characteristics of each 3D specific energy distribution. Specific energy distributions for sources of differing mean energy are characterized by Haralick measures, e.g. contrast generally decreases with increasing source energy, correlation and homogeneity are often (not always) higher for higher energy sources. Significance. Haralick texture analysis successfully quantifies spatial trends in 3D specific energy distributions characteristic of radiation source, target size, and absorbed dose magnitude, thus offering new avenues to quantify microdosimetric data beyond first order histogram features. Promising future directions include investigations of multiscale tissue models, targeted radiation therapy techniques, and biological response to radiation.

Microdosimetry, the systematic study and quantification of the spatial and temporal distribution of absorbed energy in irradiated matter (Rossi and Zaider 1996), is used for numerous experimental and computational investigations designed to advance the field of Medical Physics. For example, recent studies have demonstrated that Monte Carlo (MC) simulations are capable of providing 3D specific energy (z, defined as the energy imparted per unit mass m) distributions using realistic microscopic modelling of cell populations (Villegas et al 2013, Oliver and Thomson 2018a, 2018b). In parallel, experimental techniques are being developed for high-spatial resolution dosimetry, e.g. Raman spectroscopy in conjunction with radiochromic film (Mirza et al 2016, Mcnairn et al 2021), or microdetector arrays (Bachiller-Perea et al 2022). In general, considering microdosimetric quantities provides a complementary, microscopic perspective compared to conventional and ubiquitous dosimetric quantities such as absorbed dose (, where is the mean specific energy imparted to an infinitesimal volume of mass dm and is the mean specific energy (ICRU 2011)). The significance of microdosimetric investigations is demonstrated by its potential for supporting development of novel treatment modalities (e.g. nanotherapy involving gold nanoparticles (Zygmanski and Sajo 2016, Sakata et al 2018)), and new understandings of radiobiological effects of radiation exposure (Pater et al 2016, Villegas et al 2016, DeCunha et al 2021, Bertolet et al 2021).

Despite the importance of microdosimetry, analyses of microdosimetric distributions often rely on first-order statistics (e.g. mean and standard deviation) with little-to-no consideration of the spatial distribution of data (Villegas et al 2013, Oliver and Thomson 2018b). However, recent work introduced Haralick texture analysis (Haralick et al 1973) for the quantitative characterization of dosimetric distributions across micro- to macroscopic length scales (Mansour and Thomson 2023), focusing on examples to illustrate proof-of-concept. Initially proposed as a method to quantify the relation of neighbouring pixels within images, Haralick analysis has seen broad application for the classification of multidimensional data in fields such as image processing (Soh and Tsatsoulis 1999, Clausi 2001) or computer vision (Dollar et al 2012) and with recent applications in medical physics, e.g. radiomics (Vallières et al 2015), dosiomics (Rossi et al 2018).

Haralick analysis uses a grey level co-occurrence matrix (GLCM) to quantify the spatial arrangement of intensity values within a distribution, often pixels within an image. To generate a GLCM, observed intensity values are typically mapped to a finite number of bins, often referred to as 'grey levels' with a maximum number of grey levels (N), in a process that is referred to as 'quantization'. Many projects have been looking for optimal quantization approaches in various applications (Soh and Tsatsoulis 1999, Clausi 2002, Gomez et al 2012) and no standardized method exists. Furthermore, it has been demonstrated that Haralick measures depend on the quantization method (Brynolfsson et al 2017) and researchers have investigated the use of different quantization approaches for use within Haralick texture analyses. For example, quantization methods and sensitivity to the number of grey levels have been investigated in different contexts e.g. image classification (Soh and Tsatsoulis 1999, Clausi 2002) or radiomics (Vallières et al 2017). To address the sensitivity to quantization, Löfstedt et al (2019) developed a modified set of Haralick features with the intention of determining textural measures that are asymptotically invariant to N, while preserving interpretations of many texture descriptors. While Löfstedt et al (2019) demonstrated that the modified Haralick measures were asymptotically invariant to quantization for two datasets (comprising images from T1-weighted MRI volumes of the brain and histology images of colorectal cancer glands), this is not always the case (Garpebring et al 2018).

The present work explores the application of Haralick texture analysis to characterize 3D microdosimetric distributions of specific energy in cell-scale targets. We build on previous work (Mansour and Thomson 2023) which illustrated the potential for Haralick features to characterize microdosimetric distributions considering a single target size (cubic 3× 3 × 3 μm3 volumes) and one magnitude of absorbed dose (40 mGy) for three source spectra (125I, 192Ir, and a 6 MV medical linac). In particular, we investigate how Haralick features can quantify changes in 3D microdosimetric distributions considering varying cell-scale target sizes, 6 photon spectra, and varying magnitudes of absorbed dose. Given that previous investigations have demonstrated considerable variation in specific energies in populations of cell-scale targets with varying target volume and dose (Villegas et al 2013, Oliver and Thomson 2018b), we adopt the approach of Löfstedt et al (2019) to compute Haralick measures and assess sensitivity of computed features to the number of grey levels used in quantization.

The flowchart in figure 1 provides an overview of our methods to generate 3D specific energy distributions and then calculate modified Haralick texture measures. Similar to the work by Mansour and Thomson (2023), textural measures are calculated from quantized MC generated specific energy distributions. However, the work presented herein considers a wider microdosimetric parameter space with varying scoring voxel volumes (1–15 μm side lengths), mean specific energies (10–400 mGy) and incident photon source spectra (mean energy: 20 keV—2 MeV). The resultant expanded parameter space necessitates the use of modified Haralick analysis to reduce sensitivity to quantization. Section 2.1 describes the MC simulations used to generate the dosimetric data; the implementation of Haralick textural analysis is described in section 2.2.

Figure 1. Overview of the framework to generate microdosimetric distributions, process, and extract directionally invariant modified textural features.

Download figure:

Standard image High-resolution image 2.1. Monte Carlo simulations of 3D microdosimetric specific energy distributions

All simulations are performed using the EGSnrc (Kawrakow et al 2021b) application egs_brachy (Chamberland et al 2016), pulled from the EGSnrc_CLRP github egs_brachy branch with most recent commit 134c731. The XCOM photon cross section database (Berger et al 2010) and the NRC bremsstrahlung cross section database (Kawrakow et al 2021a) are used. Rayleigh scattering, bound Compton scattering, and electron impact ionization are turned on. The high-resolution random number generator option is used. All other transport parameters are EGSnrc defaults. The transport cutoff and production threshold for the kinetic energy of electrons and photons is 1 keV. Table 1 provides an overview of MC simulations performed (see figure 1 of the supplementary materials for a schematic diagram). A water phantom is modelled, consisting of a 40 × 40 × 40 array of cubic voxels as the scoring volume embedded in a larger scatter phantom, all with uniform mass density 0.998 g cm−3. Cell-scale scoring voxels are considered, with side lengths of 1, 2, 3, 5, 7, 9, 11, and 15 μm. Previous work has demonstrated the reliability of EGSnrc for scoring in micron-scale geometries (Oliver and Thomson 2018b, Martinov and Thomson 2020).

Table 1. Overview of MC simulations: source, phantom, scoring voxels, and quantity scored.

SourcePhantomScoring voxelsQuantity scoredparallel beam; 103Pd, 125I, 120 kVp, 192Ir, 60Co, and 6 MV spectra0.998 g cm−3 homogenous water; 40 × 40 × 40 array of cubic voxels within larger scatter phantomvoxel side lengths; 1, 2, 3, 5, 7, 9, 11 and 15 μmspecific energy;

Six photon source spectra with keV to MeV source energies are considered: 103Pd, 125I, 120 kVp, 192Ir, 60Co and a 6 MV medical linac photon spectrum, with minimum, mean, and maximum energies summarized in table 2. The 103Pd, 125I, and 192Ir spectra are distributed with egs_brachy (Chamberland et al 2016) while the 60Co and 6 MV spectra are distributed with EGSnrc (Kawrakow et al 2021b). The 120 kVp spectrum corresponds to an x-ray source with a tungsten target and 2 mm of aluminum filtration and is obtained from the Siemens x-ray spectrum simulation tool (https://bps.healthcare.siemens-healthineers.com/booneweb/index.html) (Boone and Seibert 1997). Phantom dimensions are motivated by considering electron continuous slowing down approximation range, RCSDA, for each source (Oliver and Thomson 2018b) to ensure build-up and scatter, and have side lengths of 1.0 cm (103Pd, 125I, 192Ir and 120 kVp), 3.0 cm (60Co) and 6.0 cm (6 MV). The source is a parallel beam of square cross section with side length taken to be half that of the scatter phantom.

Table 2. Summary of source spectra with minimum, mean, and maximum photon energies; CSDA range is indicated for an electron of kinetic energy equal to the source mean photon energy (ICRU 2016).

SourceMin Energy/MeVMean Energy/MeVMax Energy/MeVReference RCSDA/μm 103Pd2.70E−031.89E−024.97E−01Chamberland et al (2016)7.82E+00 125I2.72E−022.84E−023.55E−02Chamberland et al (2016)1.61E+01120 kVp8.00E−035.59E−021.21E−01Siemens Radiography (2022)5.29E+01 192Ir8.91E−033.47E−011.38E+00Chamberland et al (2016)1.05E+03 60Co5.00E−021.07E+001.34E+00Kawrakow et al (2021b)4.76E+036 MV2.50E−012.02E+006.00E+00Kawrakow et al (2021b)9.96E+03

Interaction scoring is used to compute specific energy in each voxel. The mean specific energy over all scoring voxels, , corresponds to the absorbed dose in the volume made up of all the scoring voxels. Absorbed doses between 10 and 400 mGy are achieved by varying the number of histories simulated. To estimate statistical uncertainty on absorbed dose, we replace the (40)3 array of target voxels by a single scoring volume spanning their collective volume, computing the uncertainty using history-by-history statistics (Walters et al 2002). Statistical uncertainties vary with scoring voxel volume, source spectrum, and absorbed dose magnitude, and for k = 1 range from 10% (103Pd, (1 μm)3 scoring voxel volume, D = 10 mGy) to <0.3% (all spectra, (15 μm)3 scoring voxel volume, D ≥ 150 mGy).

For each spectrum and absorbed dose magnitude considered, multiple realizations of the 3D specific energy distribution are determined by repeating MC simulations with different random number seeds; these realizations are used to assess corresponding variation in Haralick measures. The number of different realizations of specific energy distributions considered varies as a function of and is motivated by the observed variation in statistical uncertainty of absorbed dose. At =10 mGy, 50 realizations are considered. At 400 mGy, at least 4 realizations are considered. As an example of the calculation time: an 125I simulation requires 4 h to achieve 3.5 × 109 histories (D = 40 mGy, (3 μm)3 scoring voxel volume) on a single Intel Xeon 3.0 GHz CPU (model: 5160).

2.2. Haralick analysis

As part of the process to compute Haralick features, the specific energy distributions undergo a 'quantization' process (figure 1). This involves mapping (or binning) each value z from an MC-determined 3D specific energy distribution (denoted in figure 1) to an integer value to yield a 'quantized' 3D array (denoted ). The quantization approach implemented herein uses the digitize() function (from Python (Van Rossum and Drake 2009) package numpy (Harris et al 2020)) with bin delimiters , where and i = 0, 1, 2, ..., Nb . The values of and are set to the smallest and largest magnitudes of specific energy observed over all the microdosimetric datasets considered: mGy. The integer Nb defines the maximum number of quantization levels (or bins). Table 3 presents the different values of Δz, the quantization level 'width', alongside corresponding values of Nb . Sections 3.1, 3.2, and 3.3 present Haralick features determined with Nb = 2048 whereas section 3.4 assesses sensitivity to the value of Nb , considering all values in table 3.

Table 3. The maximum number of quantization levels (Nb ), and corresponding quantization level width (Δz), considered for the investigation of textural measures to quantization (section 3.4).

Nb Δz / mGy12842256215121110245.220482.640961.3

As noted in section 1, we adopt the approach developed by Löfstedt et al (2019) to compute Haralick textural measures. Their approach was developed with the goal of obtaining modified Haralick measures that are asymptotically grey level invariant, which we investigate in section 3.4. The haralick() function available in the Python (Van Rossum and Drake 2009) package mahotas (Coelho 2013) is used in conjunction with the source code provided by Löfstedt et al (2019), available on tomlof github repository with most recent commit f83acbf. These calculations involve the construction of the GLCM, Pθ . Each element in Pθ (i, j) counts the number of times an adjacency pair, adjacent elements with values i and j, appears in the quantized distribution within a displacement of one voxel and for a particular adjacency direction, θ. Thus, Pθ (i, j) is an N × N matrix, where N represents the largest value in the quantized array (N ≤ Nb ). The computation of a modified GLCM (), is outlined in Löfstedt et al (2019), and involves the explicit consideration of the number of quantization levels, N, for each respective GLCM.

The mahotas package is used to calculate symmetric GLCMs for 13 of the 26 possible adjacency directions required to compute directionally-invariant features (Mansour and Thomson 2023, Löfstedt et al 2019). The source code provided by Löfstedt et al (2019) is used to calculate modified GLCMs and textural measures. Due to a high level of correlation between textural measures (Vrbik et al 2019), we focus on five textural features: homogeneity (), contrast (), correlation (), local homogeneity (), and entropy (), where the tilde notation follows the convention of Löfstedt et al (2019):

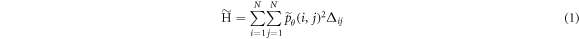
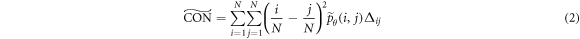
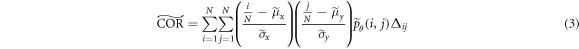
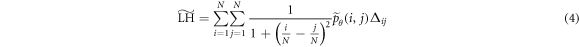
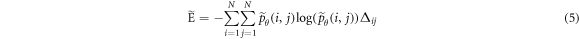
where , , , , , , , .

Löfstedt et al (2019) note that the interpretation of the modified texture features does not generally change when compared to the original measures (mainly because computation of the measures involves intermediate rescalings/renormalizations). Entropy is an exception as the modified entropy measures can be negative (Löfstedt et al 2019). A concise interpretation of the original Haralick measures is provided elsewhere (Kumar et al 2014, Vrbik et al 2019, Mansour and Thomson 2023).

In the following, we present Haralick features extracted from 3D specific energy distributions considering scoring voxels with side lengths between 1 and 15 μm (section 3.1), mean specific energies (absorbed dose) between 10 and 400 mGy (section 3.2), and 103Pd, 125I, 120 kVp, 192Ir, 60Co, and 6 MV incident photon spectra (section 3.3). The sensitivity of textural measures extracted from specific energy distributions to quantization (examining sensitivity to NB and corresponding Δz) is investigated in section 3.4. The supplementary materials for this work include additional specific energy distributions and figures of extracted Haralick measures to complement those presented herein.

3.1. Sensitivity to voxel volume

Figure 2 present