After its theoretical prediction by Leon Brillouin a century ago [1], Brillouin spectroscopy has become an important tool for investigating the mechanical properties of homogeneous materials. This technique is based on the interaction of light with the acoustic waves that spontaneously propagate inside the sample to extract information about their mechanical properties: the viscoelastic characterization occurs without any physical contact or labeling, unlike other commonly used approaches [2–6]. This peculiar characteristic made Brillouin spectroscopy a valuable technique to measure the mechanical properties of biological and biomedical samples [7–12]. However, the complex and heterogeneous nature of biological samples introduced new challenges on the interpretation of Brillouin spectra, where the mechanical information is highly intertwined with the morphology of the sample [13, 14]. This suggested a transition from single point characterization employed on homogeneous materials, to scanning-based 2D and 3D analysis. In recent years, the development of Brillouin confocal microscopes has made possible to improve the spatial resolution to the microscales, enabling the mechanical characterization on such challenging length scale [13, 15, 16]. Moreover, new experimental arrangements highly increased the measure speed enabling also the 3D mechanical characterization [17–20]. In this regard, the label-free and high-resolution features have driven the idea of exploiting Brillouin spectroscopy to correlate the samples morphology with the mechanical properties of their microstructures using the Brillouin frequency shift as a new contrast method to build images. Here we propose a more in-depth use of the information present in the Brillouin data, in particular, we used the frequency shift as well as the peak intensity to detect the interfaces between different materials in microstructured samples. We used cells in adhesion as a benchmark biological sample to test the approach, and we successfully provided the value of their thickness, analyzing the modification of the Brillouin signal passing from the glass substrate, crossing the cell and entering inside the buffer solution. Cell thickness plays a critical role in driving cell functions [21–23]. The relationship between cell size and function has a significant impact on various activities, including metabolism, nutrition intake, and biosynthesis capacity of a single cell [24–26]. For example, while mitochondrial activity increases at intermediate sizes, the rate of cell growth decreases with cell size [27]. It is interesting to note that many of these activities are influenced by the surface area-to-volume ratio rather than the cell volume itself. However, assessing cell thickness is not trivial: in some cases, it requires long sample preparation [28], prior knowledge of other sample parameters [29] or invasive experiments [22, 23, 30]. It is possible to easily address this information using Brillouin microscopy, by mapping the sample along its z-axis to locate sample interfaces. These types of measurements have already been acquired to characterize lateral resolution of Brillouin spectroscopy [31] and similar approaches are already been used for the determination of relevant biological structures in tissues [32] or to follow the time evolution of the cell size [33]. Here, we aim to describe this methodology in greater detail making consideration about how to extract information with the highest degree of accuracy.

For this investigation we used HEK293T cell line from ATCC (www.atcc.org—catalog number: CRL-3216™). Cells were cultured in tissue culture polystyrene flasks in DMEM High Glucose (Euroclone S.p.A.) supplemented with 10% fetal bovine serum (Euroclone S.p.A.), 1% penicillin-strectomycin (Euroclone S.p.A.), and 2 mM L-glutamine (Euroclone S.p.A.) in a humidified atmosphere and 5% of CO2 at 37 °C. The medium was changed every 3 d. Cells were trypsinized, seeded at a concentration of 5 × 103 cells ml−1 in glass coverslips and cultured in the growth medium. Then, cells were fixed with 4% paraformaldehyde for 20 min at room temperature (RT) and washed with PBS. For Brillouin measurements, the glass coverslip was inserted in a sample holder designed specifically to keep the cell hydrated in PBS during the measurements.

The same fixation protocol was applied to prepare samples for fluorescence imaging. Fixed samples were after permeabilized in 0.1% Triton X-100 for 5 min at RT, washed with PBS and blocked for 30 min in 1% bovine serum albumin (BSA). Alexa Fluor 488 Phalloidin (Thermo Fisher Scientific, Waltham, MA, USA) diluted appropriately (1/250 on 1% BSA) was added to the samples to stain f-actin. Samples were left incubating in the dark for 1 h, before being washed 2 times with 0.5% Tween-20. Finally, samples were mounted into glass slides using VECTASHIELD mounting medium (Vector Laboratories).

Brillouin spectra have been acquired using the high-contrast version of the tandem Fabry Perot interferometer (TFP2 HC JRS Scientific Instruments, Tablestable Ltd, Mettmenstetten, Switzerland). The details of the instrumental set-up are reported in [34]. In brief, the laser beam (Spectra Physics Excelsior) with a wavelength of λ = 532 nm is focused on the sample with a power of 15 mW. A water immersion objective (UPLSAPO 60XW, Olympus, NA = 1.2) is used to focus and collect the backscattered light, which is sent to the interferometer (figure 1(a)).

Figure 1. (a) Schematic of the acquisition system: laser beam is focused and collected through the same objective. Sample is observed through an inverted microscope while it is kept hydrated by using a self-designed sample holder. Scattered light is then sent to the Brillouin interferometer. (b) Bright Field image of a HEK293T cell. Scale bar = 10 μm.(c) Stokes side of a representative Brillouin spectrum acquired for a point inside the cell (dots) compared with its DHO fit (solid line).

Download figure:

The Brillouin microscope provides an effective magnification of 50X. In the optical configuration here used, the achieved spatial resolution is 0.5 μm and 3 μm in the lateral and axial directions, respectively. The spectral resolution of the HC-Tandem Fabry–Perot interferometer is about 100 MHz while the free spectral range (FSR) can be adjusted by selecting the appropriate mirror spacing, d. In the present case, a mirror spacing of d = 10 mm was chosen, providing us a FSR of 13 GHz. In this condition, it was possible to measure the whole Brillouin peak, typically located at around 8 GHz. The two FSRs, acquired in the Stokes and anti-Stokes side of the elastic line, were measured across 512 channels, yielding a sampling step of around 50 MHz. Thanks to the use of an inverted microscope coupled to the interferometer, we can also acquire bright field images in transmission obtaining good quality images of cells (figure 1(b)).

For the mapping measurements, the microscope objective is mounted on the motorized Precision Linear Stage PLS85 (PI miCos), allowing the scans along the z direction. Maps were acquired by choosing a step size of 1 μm, starting by focusing the laser spot on the glass coverslip, crossing the cells and finishing by focusing the laser spot on the buffer media above the cell. We developed a Python software capable of automatically moving the objective after each acquisition, obtaining a fully automated procedure for the acquisition of the maps. Each measure was acquired for 10 s, to allow good data quality also for very low intensity cell spectra at the cell-glass interface. In this case, thanks to the high contrast of the TFP2 HC interferometer, it was possible to follow the transition of the scattering volume from the cell to the coverslip without any additional background, even in the presence of strong elastic scattering from the glass surface. Scans were performed on many cells (N = 17) stochastically chosen within the sample. For each scan, the position chosen in the x–y plane was the center of the nucleus. With this method we aim to extract the maximum cell thickness.

Data analysis was performed using a custom-made Python script. Brillouin spectra were fitted using a damped harmonic oscillator (DHO) function:

where the fit parameters are ωB, Γ and I0, respectively, the Brillouin frequency shift, peak width and peak intensity. This function has been convoluted with the response function of the experimental setup. In particular, we took into account the peak broadening induced by the finite resolution of the FP spectrometer as well as the spread on the scattering wavevector q induced by the use of high NA objectives [34].

The 3D fluorescence microscopy images were acquired with LSM900 with Airyscan 2 (Karl Zeiss, Jena, Germany), using a 40x Plan-Apochromat oil immersion objective with 1.3 NA. The sample was excited using a 493 nm laser and the light collected using the Airyscan sensor [35]. For each cell, a full z-stack was collected, choosing the optimal parameters to maximize the resolution (a step size of 38 nm for x and y axis and 170 nm for z axis). Scans were acquired for 21 cells that, like for Brillouin measurements, were stochastically chosen within the sample to obtain the thickness distribution. Airyscan post-processing was carried out from ZenBlue Software (ZEISS), involving a linear deconvolution of the 32 individual elements of the detector and a pixel reassignment of each element to the center position [36]. We obtained a planar resolution XY of 120 nm and an axial resolution Z of 350 nm. The cell thickness was extracted from cells by analyzing the orthogonal view images using the open software Fiji [37]. Again, a point on the center of each nucleus was chosen in the x–y plane to measure cell thickness; 6 measurements were acquired in the XZ and YZ planes (see figure 3 for an example), and average was chosen as the final value.

The data reported in figure 2 shows the evolution of the Brillouin peak during the linear scan along the z-direction. The acquired spectra (dots) are reported together with the corresponding DHO fit (solid line). The first interface -between cell and glass coverslip (condition A in figure 2(a))—is accompanied by the gradual variation of the measured peak intensity (figure 2(b)—spectra marked in red). On the other hand, when crossing the interface between the cell and the buffer (condition C in figure 2(a)), the frequency shift deviated towards lower frequencies, as highlighted by the black dots showing the maximum of the peak intensity in figure 2(b). For the first interface (glass-cell), since the Brillouin peaks of the cell and the glass are well separated—centered at around 8 GHz and 30 GHz, respectively—it is not expected any modification in the peak shape or position, but the decreasing percentage of cell content inside the scattering volume can be followed as a decrease of the peak intensity, I0. This method can be used to locate the interfaces between two materials characterized by high acoustic mismatch or in general when the two peaks can be well separated in the fitting procedure. Conversely, for the second interface (water-cell), we analyze the evolution of the frequency shift, ωB. The Brillouin peak of the cell, although centered at different frequency, is very close to the peak of the buffer so the two contributions are merged within a unified band and the evolution of ωB contains the information on the filling fraction of the different components in the scattering volume. The choice to use a single peak instead of two, extends the applicability of the method even in the presence of hybridization of the acoustic modes between two regions characterized by low acoustic mismatch. A similar approach based on the extraction of a single frequency parameter accounting for multiple contributions, involves monitoring the evolution of the first order spectral moment. This latter method has been already used to visualize the sample micro-structures even in the case of well separated Brillouin peaks [38].

Figure 2. (a) Schematic of some of the laser spot positions during the scan: respectively, first interface (A), cell center (B), second interface (C). (b) Brillouin spectra (dots) acquired from a representative cell together with their DHO fit (solid line). Each spectrum represents a position in the z scan (from coverslip to buffer starting from the bottom, with 1 μm step size). Interfaces can be identified by looking at the frequency shift (black dots that indicate the maximum of the peak intensity) and peak intensity (spectra marked in red). Labeled spectra correspond to the three laser positions shown in panel (a).

Download figure:

In figure 3(a), we plotted the value of I0 and ωB as a function of the z-position, while crossing the two interfaces. Assuming a sharp interface and a Gaussian profile of the spatial (axial) resolution with variance σ2, the resulting edge spread function, obtained by convolution, that describes the transition of both parameters I0 and ωB, is an error function (erf), centered at the interface position [31, 34]:

Figure 3. (a) Peak intensity (red squares) and frequency shift (black dots) plotted as a function of z-position (with z = 0 on the x-axes corresponding to the glass-cell interface) together with their erf fits (solid red and black line). The y-limits of the two y-axes have been adjusted to align the y-positions of the two fit plateaus, enabling the graphical representation of the cell thickness as a horizontal line (green dashed line) that connects the two interface positions. (b) Evaluated cell thickness for all the analyzed cells. Each point is reported with its experimental error bar. (c) Mean frequency shift evaluated from erf fitting parameters. Each point is reported with its experimental error bar.

Download figure:

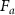The other fitting parameters are , the reference value of the parameters at the interface and Δ the total variation of the investigated parameter across the interface. This function has been used to fit separately the two transitions and the cell thickness is obtained from the fitted values. This procedure has been carried on for the analysis of all cells and the so obtained values are reported in figure 3(b). Here, the errors for have been evaluated as the square root of the diagonal element of the best-fit covariance matrix, then these have been propagated accordingly to obtain the error for thickness. In our case, the errors are always below 230 nm, being the uncertainty in about ∼100 nm. This value is smaller than either the chosen scan step size (1 μm) or the axial resolution. Therefore, the fitting procedure, which takes into account the entire scan and the evolution of numerous spectra, allowed us to locate the interface positions with higher spatial resolution with respect to the resolution of the technique [13, 31]. By evaluating this evolution, the accuracy is enhanced, even overcoming the physical limit given by the wavelength of the investigated phonon (∼200 nm). This super-resolution effect is due to the localization procedure which is feasible when the presence of an interface is known in advance, as already shown for similar techniques [39, 40]. This does not affect the actual resolution of Brillouin spectroscopy, which refers to the length scale for which it is possible to measure accurately the mechanical properties of a heterogeneous material. Instead, the spreading of the cell thickness values (STD = 1.3 μm) can be assigned to the intrinsic morphological distribution of the cells as already observed using different methods [29].

By evaluating f(z) far from the interface, we can also extract the mean frequency shift for the analyzed cells. Therefore, the technique offers the opportunity to obtain additional information correlating the sample morphology and the mechanical properties at once. The data here obtained is reported in figure 3(c). While it is recognized that in case of osmotic treatments or substrate alterations, variations in cell thickness are also accompanied by variations in the cell mechanics [41], we did not observe a clear correlation in our study. The lack of correlation could be expected in this context, since the cells were not subjected to any specific treatment. In any case, the correlative analysis here proposed can be instrumental in understanding how processes involving morphological modifications, such as drug treatment, disease progression, microenviroment modifications can affect cell mechanics. By examining the relationship between morphological changes and mechanical properties using a single microcopy technique, new insights into cellular behavior can be gained.

To validate the here proposed procedure, we used the 3D images obtained from the cells by confocal fluorescence microscopy. Also, in this case, the image post-processing plays a crucial role in enhancing the resolution of the collected images. In fact, the Airyscan processing exploits the data extracted from the 32-element detector to reconstruct the image with better resolution by a numerical deconvolution process [42]. It is interesting to note that both the procedures just outlined and the one designed for Brillouin analysis (more similar in principle to single molecule localization microscopy [43]), exploit a priori knowledge about the expected signal profile to locate objects with higher resolution.

Figure 4(a) reports a representative orthogonal view of an acquired z-stack. Here, we used the signal of the fluorophore linked to actin fibers to extract information about the cell thickness on x–z and y–z planes. The obtained values have been compared with the ones extracted from the Brillouin analysis (figure 4(b)). No significant differences can be found between the two distributions (unpaired two-tail t-test, p > 0.05), indeed proving our method to be reliable to measure sample thickness. In principle, with this method, it is possible to extract size information not only for adherent cells but in every configuration, including samples embedded in 3D environments. This overcomes the main limit of AFM, that can allow thickness extraction, but only when the sample surface and substrate level are both accessible. Moreover, the label-free characteristic of the method, enables a quick thickness characterization unlike fluorescence microscopy, where the measurement does not require much time, but involves a long sample preparation. Furthermore, the high accuracy achievable also between materials with similar acoustic properties, can provide an advantage with respect to other methods which need high mismatch—in terms of refractive index or acoustic properties—between the investigated structures and their environments [44, 45]. This method can be applied regardless of the Brillouin acquisition system (VIPA, TFP, SBS), as long as it is possible: (i) to measure a variation in the frequency shift of the Brillouin peak during the transition between two materials, when they are characterized by similar Brillouin shift and/or ii) to measure the variation in the Brillouin scattering intensity when a given material leaves the scattering volume. The only parameter that must be taken into account to evaluate the correct value of the sample size is the Brillouin spatial resolution, ensuring that it is possible to acquire the entire shape of the erf function before crossing another interface. Indeed, the spatial resolution is the parameter that determines the slope of the transition (σ) [31]. In this study, the fixation on samples measured with Brillouin spectroscopy has been performed to allow a consistent comparison with confocal microscopy data. In fact, for measuring the thickness by fluorescence microscopy, cells were fixed before labeling their structures. However, the time required for the total Brillouin scan is compatible with measurements of living samples. Measurements on a few live cells are presented in the supplementary material, where the same method for the data treatment has been applied (figure S1), yielding thickness results that fall within the thickness distribution.

Figure 4. (a) Orthogonal view of a confocal stack obtained on a representative HEK293T cell. The fluorescence signal is associated to phalloidin bound to the actin cytoskeleton. Thickness was obtained from images by quantification of the XZ and YZ sections (red bars). (b) Comparison between cell thickness evaluated from Brillouin measurements (the same data is reported in figure 3(b)) and fluorescence microscopy. Data were analyzed by an unpaired t-test, with no significant difference between the samples with p > 0.05.

Download figure:

Brillouin spectroscopy is emerging as a powerful tool to extract viscoelastic properties at the microscale. However, here we demonstrated that it is also possible to exploit the information contained in a set of spectra to extract relevant morphological parameters of micro-structured samples with high spatial resolution. In fact, thanks to the different mechanical properties between the microstructures, Brillouin spectroscopy can provide information about the morphology that can be correlated with the mechanical properties themselves.

We showed how to exploit Brillouin spectroscopy to extract information about cell thickness by analyzing the change in the Brillouin frequency shift and peak intensity, with a method that can be adjusted to work for every kind of sample. Indeed, both parameters can be selectively employed, contingent upon the width and frequency shift of the Brillouin peaks of the two components relative to the frequency resolution of the spectrometer. Cell thickness is an information of biological relevance, and its measurements pose challenges using the existing techniques. Brillouin spectroscopy allows the evaluation of this parameter without any sample preparation also in living cells. In principle, this method could be employed also for monitoring modifications over time, in particular cellular rearrangements occurring on timescales compatible with the acquisition time. This correlative analysis of thickness and mechanical properties can help us better understand the relationship between cell mechanics and cell morphology.

This work has been partially funded by the European Union—NextGenerationEU under the Italian Ministry of University and Research (MUR) National Innovation Ecosystem Grant ECS00000041—VITALITY (CUP J97G22000170005 and CUP B43C22000470005). We acknowledge Università degli Studi di Perugia, CNR and MUR for support within the project Vitality, moreover we thank the European Union — NextGenerationEU — Prin PNRR Grant P2022RH4HH — COMBINE (CUP/CUP Master B53D2302864 0001) and PRIN 2022 — CODIR (CUP J53D23001370006, CUP Master B53D23003990006). The authors acknowledge the Royal Society International Exchange program IEC\R2\202232.

The data that support the findings of this study are available upon reasonable request from the authors.