Off-the-shelf optical systems design enabled by an evolution strategy: front stop case

Commercial off-the-shelf optics enable economic and rapid solutions in the photonics industry and academia. However, the design of optical systems with off-the-shelf optics is a time-consuming task for experienced optical designers and hopeless for novice designers. In this paper, we propose an automatic optical design tool to generate optical systems using only off-the-shelf optical components without human assistance. Our solution is based on an evolution strategy (ES) that performs a discrete combinatorial optimization following optical design-based methodologies that satisfy user-defined specifications. Unlike the conventional methods, the algorithm decreases the design process time and provides optical designers with several optical solutions from where to choose and adapt for targeted applications. In this work, the ES is described and tested with front stop optical configurations. We demonstrate the broad solution domain of the algorithm through the generation of optical systems with F-numbers within a range F/1 to F/90 and field of views up to 300 mm at the image plane. To analyze the solution domain and the characteristics of the solution, we used the design specifications of 29 commercially available scan lenses and compared the performance of different ES parameters. The compatibility of our algorithm with (standard) commercially available optical design software unlocks automatic design tools for off-the-shelf optical systems.

Commercial off-the-shelf (OTS) optics are optical elements fabricated in quantity and kept in stock by optical suppliers. Due to their readily availability and low-cost, these optical elements reduce the prototyping, fabrication, assembly costs and time of optical systems, and thus, enable economic and rapid solutions for industry and academia [1–6].

However, the design of optical systems that consist completely or partially of OTS optics is a challenging task. On one side, due to the unreachable amount of lens combinations, e.g. a lens system typically consists of at least three lenses to fulfil the desired performance, and the number of lenses available in stock catalogues readily exceeds thousands of lenses, thus the number of combinations as obtained by equation (1) are possible,

Equation (1)

On the other side, the available design approaches are based on an iterative process that requires in depth expertise in optical design, and know-how in working with commercial optical catalogues (see chapter 21 from [7] and chapter 15 from [8]).

In contrast to the several algorithms that have been proposed to automatically generate starting design points of customized optical systems [9–19], only few computational methods have been demonstrated in the design of OTS optical systems. For example, the substitution method described in [7] is supported by commercially available optical design software with their integrated lens matching algorithms [7, 8]. This type of algorithms find individual stock lenses based on the optical specifications of customized designed lenses [20–23]. Although it is the current available tool in optical design software, its success ratio is limited, and in order to work properly, it strictly depends on initial customized optical systems, stressing the need for a high level of expertise in optical design.

More recently, the design of OTS optical system (OTS-OS) has been tackled as a combinatorial problem assisted by a set of deterministic rules, and a constant and automated interaction with stock catalogues. These approaches aim to explore lens combinations and to automate the design process to provide accessible methods to a novice lens designer. To the best of the authors' knowledge, the combinatorial optimization problem derived from OTS-OS design has been tackled by few works that have used 'brute force' combinatory of the stock lenses [24], iterative combinations assisted with determinist rules [25], or global and local optimizers from commercial available optical design software applied over starting points designs [26]. Although these solutions tackle, in principle, what can be considered as the core goal of OTS-OS design, the combinatorial problem of optimally searching OTS-OS still remains open. The open challenges highlight the dependence of current solutions on specific configurations [24, 25] or starting points [26], the long computing times as found in the 'brute force' method [26], and the limited exploration of the combinatorial space of splitting [25] and the global-local optimizers [26] methods.

Algorithms that generate OTS-OSs based on combinatory operations propose a novel approach and boost solutions towards automatic OTS-OSs generation. Furthermore, the previous methods point out that not only splitting operations influence the optical performance in OTS-OS, an already known practice in optical design to correct aberrations, but others operations can influence and boost the optical performance improvement within the search [19, 25]. Finally, a combinatory approach shows that the pool of solutions is highly influenced by the initial systems and the strategy implemented for choosing the initial systems and the stock lenses. This suggests that the selection strategies must be carefully analyzed for the OTS optical design problem, which is lacking in state of the art. In summary, the characteristics that make the optimization of OTS-OS a complex problem include its large solution space (Ni), its multiple specifications, the large number of local minima, and its dependence on initial optical configurations.

Evolution strategies (ESs) are evolutionary algorithms widely used to solve discrete or combinatorial optimization problems in real world applications [27–29]. Among the ESs multiple capabilities that provide combinatorial problems such as OTS-OS optimization with a practical solution include: (i) ESs evolve the search space from a population of candidates, not one particular candidate. (ii) ESs use random or probabilistic transitions to generate new candidates and apply transformations, thus reducing the probability of bias due to the influence of initial configurations. (iii) ESs can handle a large number of local minima and reduce the likelihood to converge to a local minimum. (iv) Although ESs do not guarantee to find global optima, ESs provide an efficient set of multiple solutions that represent significant improvements. These capabilities have been applied and demonstrated in many applications [30, 31], however, strategies applied in the design of OTS optical systems lack and are needed in the state of the art.

In this paper, we introduce an evolution strategy (ES) to solve the OTS-OS optimization problem. This is the first ES implemented for the automatic design of optical systems that are generated from available stock lenses. The stochastic exploration of the solutions is realized by introducing additional operators that can use a limited number of lenses, and trigger the interaction with the lens catalogue. This approach differs from those of state-of-the-art [22, 23, 25]. Due to more available operators, the proposed ES provides a deeper exploration of optical configurations, thus opening the search space of the combinatorial solutions and delivering solutions for different optical specifications. In addition, we study the dynamics and the influence of two of the main operators (crossing and splitting) probabilities on generating successful OTS-OSs. Because of the extension of the work and without loss of generality, we focus only on lens scanning systems, but we provide clear clues to extend our algorithm for other optical configurations, specifically relative to the stop position. Finally, we test and compare our implementation with a list of commercial scan lenses, for which our algorithm successfully finds OTS-OSs for their specifications.

This paper describes our method and summarizes our findings as follows. First, section 2 describes the OTS optical design problem and section 3 the ES used to solve the problem. In section 4, the algorithm is described. In section 5, first we set as a reference one commercial scan lens and analyze the parameters that influence the number and characteristics of the solutions. Second, we test and compare the algorithm with the specifications of 28 systems. Finally, the conclusions are presented.

A lens system consists of individual lenses, also referred to as lens elements, that are described by the radii of curvature, thickness, diameter and glass type. Those parameters are used by the optical designer in combination with the airspaces, refractive indices and dispersive powers of multiple elements, the position of the stop or aperture-limiting diaphragm as available design 'degrees of freedom'. The degrees of freedom are used to reduce the aberrations of the optical system and maintain the required design specifications such as focal length, magnification and f-number of the lens system [7]. Contrary to customized lens design, in the OTS-OS design problem, such degrees of freedom are represented by a discrete domain of solutions generated by available commercial stock lenses, thus limiting the possible values used in the OTS-OS optimization.

The OTS-OS design aims to find a combination of commercial stock lens elements to compose an optical system that satisfies the user's technical specifications [22, 23, 25]. Those specifications are defined by the main application of the target system and used as control parameters of the ES. At the same time, the target system determines the strategy to propose the initial systems. Here, we focus on optical systems in which the stop is located outside the lens system. Therefore, we propose initial optical systems based on positive and negative lenses to compensate for the aberrations and fulfil the design specifications. Although the initial configurations depend on the target system, the ES and the mutation operators applied over the candidates follow established rules independent from the optical system. Therefore, our method searches for new candidates based on their constant mutation and iterative competence.

3.1. Target systems

Based only on the position of the aperture stop, we classify the optical systems in three possible configurations. The first type locates the stop in front of the first lens element. This configuration includes scan lenses, telescopes and landscape lenses. The second type positions the stop between two lens elements and consists of many optical systems, e.g. projection lenses, camera objectives and microscope objectives, among others. Finally, the stop at the rear of the optical system represents the last type of systems, including, for example, eyepieces. In terms of stop position, the first and last types are analogous configurations and the design process to obtain both systems is similar [32].

We implemented and tested our ES for systems of the first type, the front stop case. Figure 1(a) illustrates this configuration with a scan lens that consists of a front stop, double convex, double concave and plane convex lenses. To represent a candidate for these optical systems, we define the vector L of stock lenses lj as

Figure 1. (a) Sketch of a scan lens with power configuration $[-,+,+]$ representing the target system (S: stop, SP: scanning/image plane, SL: scan lens, s.d.: scanning distance, w.d.: working distance). The red and blue lines represent two light fields. (b) Spot diagram of one light field that illustrates the control parameters used in this work.

Download figure:

Standard image High-resolution image Equation (2)

being the relative position of each element in the vector the same as its corresponding real optical element in the OTS-OS.

3.2. Control parameters

Besides the location of the stop with respect to the lenses, other parameters that define the target optical system include the paraxial, physical specifications and the maximum aberrations allowed. First, the paraxial specifications are primarily defined by: (i) F-number (F/#), (ii) effective focal length (EFL), (iii) entrance pupil diameter (EPD), (iv) the paraxial field of view (FOV) at the image plane and (v) the source wavelength [32]. For scan lens design, the system is set in this algorithm as monochromatic, and the source wavelength to be used with the scan lens is set as the target value.

As physical specifications (constraints), we set the maximum and minimum values for the (vi) lens diameters, (vii) the airspace between the stop and the first optical surface, named scanning distance; (viii) the airspaces between lenses, and (ix) the working distance. The latter is defined as the distance between the last optical surface and the image or scanning plane. Finally, the performance of the optical system is measured with (x) the root mean square (RMS) spot size at the image plane, (xi) the amount of f-theta ($f-\theta$) distortion, and for telecentric systems, (xii) with the incident angle of the chief ray at the image plane [33], figure 1(b). The smaller these values (parameters x) to (xii), the better the overall performance of the scan lens. Figure 1(b) illustrates the rays' distribution on the image plane for one field after raytracing simulations. The difference between the paraxial chief ray and the real chief ray determines the amount of $f-\theta$ distortion, the RMS variance of the rays' position is calculated with respect to the chief ray and compared with the diffraction-limited spot radius (Airy radius).

The technical and performance parameters (previously listed from (i) to (xii)) for all the candidate systems are evaluated and stored in the control parameters vector y as the variables yi as shown in equation (3),

Equation (3)3.3. The ES

For optical design, the goal of the ES is to minimize an objective or merit function F with respect to a set of decision variables or control parameters y, as defined by equation (3), by performing a series of transformations on the population of optical systems and selecting the most fit candidates from the current population. These selected candidates are carried forward into the next generation population. Following the Beyer and Schwefel notation [34], the ES operates on populations $\mathfrak$ of individuals $\mathfrak$. An individual $\mathfrak_m$ with subindex m includes, for our problem, not only the control parameters ym and its merit function value $F_m: = F(\mathbf_m)$, but also the optical system candidate Lm of equation (2) and a set of strategy parameters sm . The strategy parameters sm are used to control the mutation operators that produce a new generation of offspring $\mathfrak_o$ of OTS-OSs. Our ES is based on the $(\mu/\rho+\lambda)$- ES with ρ = 1 (no recombination) [34]: a population of λ-offsprings individuals $\mathfrak_o$ is generated from the set of µ-parent individuals $\mathfrak_m$ by copying the parental set and performing on them a series of mutations. After the population of offspring is completed, a pool of $\gamma = \mu+\lambda$ OTS-OS candidates, with $\lambda = \mu$, is used in the selection of a new generation of OTS-OSs. This process guarantees that only the best $\gamma/2$ OTS-OS are chosen and transferred into the next parental generation $\mathfrak^+1)}_p$. As follows, we describe the process to initialize the parental population $\mathfrak^ = 0)}_p$, the mutation operations established for our particular ES, and the evaluation, selection and termination conditions.

3.3.1. The population $\mathfrak_p^ = 0)}$

The initial candidates consist of OTS-OSs of three singlets, one negative and two positive focal length lenses. The combination of positive and negative lenses was chosen to compensate the Petzval curvature and $f-\theta$ distortion, and to provide enough scanning distance to place a scanning device at the stop of the OTS-OS [33]. The scan lens candidates of the initial generation are based on two lens configurations, $[+,+,-]$ and $[-,+,+]$. The user can choose either one of these options or generate an equal-distributed population of the combination of both configurations. Figure 1(a) illustrates a $[-,+,+]$ configuration. Due to the limited quantity and shapes of negative lenses in commercial catalogues, our method selects the positive lenses based on the mean focal length of the negative lenses within the catalogue as follows: first, the algorithm filters the catalog according to the required lens aperture sizes. Afterwards, it calculates the mean power $\bar_$ of the negative lenses left and it searches for the µ negative stock lenses with the closest power to $\bar_$. The power of the positive lenses is calculated by using the paraxial approximation equation (4), where φ is the optical power of the target system. Once the set of positive and negative lenses are selected, the population of initial parental candidates $\mathfrak_p^$ is built by a random combination of one negative and two positive lenses following $[+,+,-]$, $[-,+,+]$ or both configurations,

Equation (4)3.3.2. Mutation operators in the OTS design problem

From the parental population $\mathfrak^)}_p$ at generation $\mathrm$, a new offspring is created by applying a set of transformations or mutation operators, as shown in figure 2. These operators are based on the actions commonly used by optical designers to improve an optical system such as splitting, swapping, inverting and permuting a lens element. In addition, we use the ES crossover to combine lenses between two parents. From all the mutation operators, splitting is an operator defined with a deterministic rule. As illustrated in figure 2, it splits the most optical-powerful lens into two randomly chosen lenses from a set of µ lenses with half of the original power. This procedure reduces the curvature of the optical surfaces, the angles of incidence and the aberrations' effect [35, 36]. Splitting a lens significantly contributes to increasing the performance of the optical system and becomes an important tool for fast systems, namely small $F/\#$. However, when only the split operator is used in the strategy, the solutions tend to have a large number of lenses that lead to increased costs and inferior performance due to an overall sensitivity to the tolerances of the optical system. As shown in figure 2, we implemented additional operators to increase the stochastic exploration of systems with a limited number of lenses and to increase the interaction with the lens catalogue, a proposal that differs from those of state-of-the-art [22, 23, 25]. For example, the swap and inverse operators are mutations executed only over the original parent. The swap operator exchanges the position of two lenses from their original configurations, leading to different configurations from the initially proposed in subsection 3.3.1. The inverse operator rotates an element 180 degrees with respect to its transverse axis. Alternatively, the crossover and permutation operators allow the interaction between other parents and the catalogue, respectively. The crossover operator combines one lens between two parents, generating two new offspring OTS-OS for each couple. The permute operator selects one element from the parent and randomly changes it with one lens with similar power from the catalogue. All the selection actions are randomly based except for the selection of the most powerful lens in the case of splitting operation. Additionally, the repetition ratio of a specific mutation operator is controlled by the strategy parameters sm, discussed in section 4.

Figure 2. Mutation operators used in the evolution strategy.

Download figure:

Standard image High-resolution image 3.3.3. Merit function and local optimization

After the mutation process, the offspring population $\mathfrak^)}_o$ is given as a list of lenses and relative positions within the optical configuration. The airspaces between all the elements of each offspring, including the stop, are optimized to get a local minimum of the merit function value. The merit function uses the square difference of the measured and the target value of the control parameters defined in section 3.2 to quantify the fitness of the OTS-OS (e.g. F/# , EFL, RMS spot size, etc). These differences are weighted by factors Wi. Besides the specifications of section 3.2, the merit function also measures the un-vignetting ratio vfield of rays for three fields. Vignetting reduces the amount of energy incident on the target plane; thus, the algorithm penalizes those systems when a percentage of rays from any field falls outside the lens apertures [20]. The merit function is set as

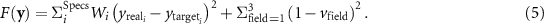
Equation (5)

Where the value $y__i}$ corresponds to the control parameter evaluated by ray tracing algorithms. Each value is then compared with the target specifications $y__i}$. For reference, a value of $v_} = 1$ means zero vignetting for the specific field.

The local optimization is iteratively performed using the damped least squares optimization algorithm until $\Delta F(\mathbf) \lt 0.01 \%$. Our experiments show that this optimization takes less than 0.5 min per candidate, when running in a CPU i7-4790 3.60 GHz with 8 GB RAM. Until this point, the offspring population $\mathfrak^)}_o$ comprises not only each list of stock lens references, but also the lens separations for which the OTS-OS perform with a merit function value

View original article
JOURNAL OF PHYSICS-PHOTONICS

Comments (0)

No login
gif
format_indent_decrease